정규화 (Normalization)
정규화는 데이터베이스 설계 과정에서 데이터를 효율적으로 분리하여 중복을 줄이고, 무결성을 유지하기 위한 방법입니다. 정규화의 목표는 데이터 중복을 없애고 데이터 일관성을 보장하는 것.
중복 데이터를 허용하지 않음으로써, 무결성을 유지하고, DB 저장 용량도 줄일 수 있다.
정규화는 여러 단계로 나뉘며, 각 단계는 정규형 (Normal Form)이라고 부릅니다. 가장 일반적으로 사용하는 정규형은 1~3 정규형이다.
1. 제 1 정규형 (1NF)
제 1 정규형은 "각 컬럼이 원자값(Atomic Value)을 가져야 한다"는 규칙.
즉, 각 열의 값은 더 이상 나눌 수 없는 단일 값이어야 하며, 복합적인 값이나 리스트, 집합 등을 컬럼에 저장할 수 없다.
예시:
학생ID 학생이름 수업명
| 1 | 홍길동 | 수학, 영어 |
| 2 | 이영희 | 수학, 과학 |
위와 같은 테이블에서는 "수업명"이 복합적인 값(수학, 영어, 수학, 과학)을 가집니다. 이를 1NF로 변환하려면, 각 수업을 별도로 분리하여 하나의 값만 들어가게 해야 한다.
1NF 변환 후:
| 학생ID | 학생이름 | 수업명 |
| 1 | 홍길동 | 수학 |
| 1 | 홍길동 | 영어 |
| 2 | 이영희 | 수학 |
| 2 | 이영희 | 과학 |
이렇게 각 값이 원자적(Atomic)인 값으로 변경되어야 제 1 정규형을 만족합니다.
2. 제 2 정규형 (2NF)
제2 정규화란 제1 정규화를 진행한 테이블에 대해 완전 함수 종속을 만족하도록 테이블을 분해하는 것이다. 여기서 완전 함수 종속이라는 것은 기본키의 부분집합이 결정자가 되어선 안된다는 것을 의미한다.
예시:
학생이 여러 수업을 듣는 경우, 학생ID와 수업ID를 기본 키로 가정한 테이블이 있다고 가정해보자.
| 학생ID | 수업ID | 학생이름 | 성적 |
| 1 | 101 | 홍길동 | 3.5 |
| 2 | 103 | 이영희 | 4.0 |
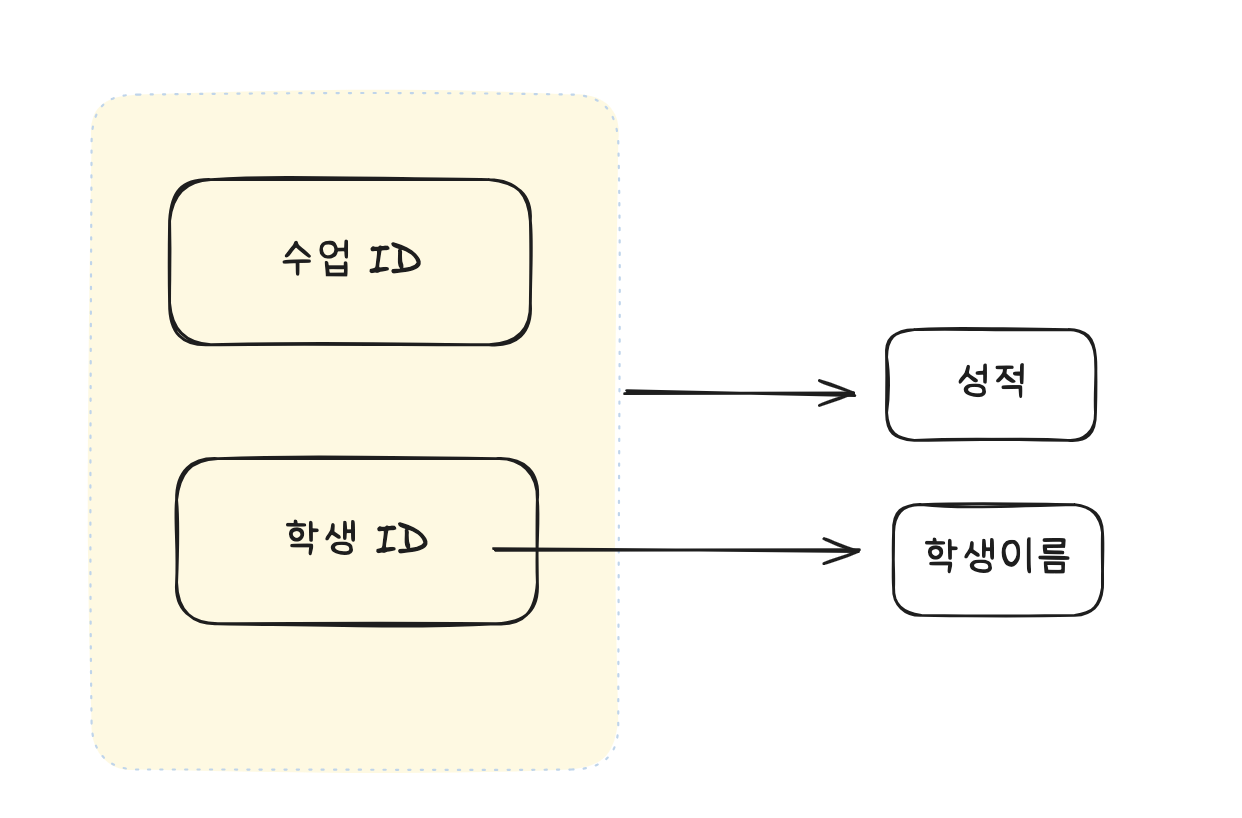
이 테이블에서 기본키는 (학생ID, 수업ID)로 복합키이다. 그리고 (학생ID, 수업ID) 기본키는 성적을 결정하고 있다.
그런데 여기서 교수이름이라는 컬럼은 기본키의 부분집합인 수업ID에 의해 결정될 수 있다. 그리고 학생이름이라는 컬럼도 기본키의 부분집합인 학생ID에 의해 결정될 수 있다.
즉, 기본키 (학생ID, 수업ID)의 부분키인 수업ID와이 결정자이기 때문에 위의 테이블의 경우 다음과 같이 기존의 테이블에서 강의실을 분해하여 별도의 테이블로 관리하여 제2 정규형을 만족시킬 수 있다.
2NF 변환 후:
- 수강 테이블:
| 학생ID | 수업ID | 성적 |
| 1 | 101 | 3.5 |
| 2 | 103 | 4.0 |
- 학생 테이블:
| 학생ID | 학생이름 |
| 101 | 홍길동 |
| 103 | 이영희 |
3. 제 3 정규형 (3NF)
제 3 정규형은 2NF를 만족한 상태에서 "이행적 함수 종속성(Transitive Dependency)을 제거해야 한다"는 규칙. 이행적 함수 종속성은 A -> B, B -> C일 때 A -> C가 성립하는 경우를 의미한다.
즉, 컬럼 간에 간접적인 종속성이 존재하면 이를 제거해야 한다.
예시:
| 학생ID | 지도교수 | 학과 |
| 1 | 김교수 | 컴퓨터학과 |
| 2 | 박교수 | 수학과 |
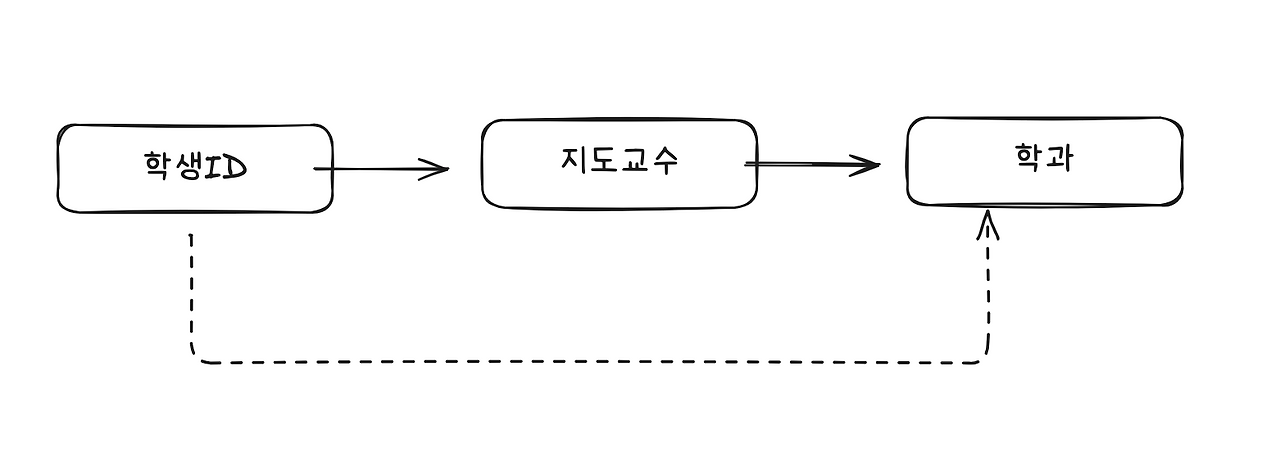
기존의 테이블에서 학생 ID는 지도교수를 결정하고 있고, 지도교수는 학과를 결정하고 있다. 그렇기 때문에 이를 (학생 ID, 지도교수) 테이블과 (지도교수, 학과) 테이블로 분해해야 한다.
이행적 종속을 제거하는 이유는 비교적 간단하다. 예를 들어 1번 학생의 지도교수가 박교수로 변경되었다고 하자. 이행적 종속이 존재한다면 1번의 학생의 지도교수님은 수학과가 되게 된다. (컴퓨터학과임에도)
3NF 변환 후:
- (학생 ID, 지도교수) 테이블
| 학생ID | 지도교수 |
| 1 | 김교수 |
| 2 | 박교수 |
- (지도교수, 학과) 테이블
| 지도교수 | 학과 |
| 김교수 | 컴퓨터학과 |
| 박교수 | 수학과 |
반정규화 (Denormalization)
반정규화는 정규화된 데이터베이스에서 성능을 향상시키기 위해 일부러 데이터를 중복하여 저장하는 과정이 이다. 이는 주로 조회 성능을 최적화하기 위해 사용된다. 데이터 중복이 발생할 수 있지만, 조회 속도를 빠르게 하는 장점이 존재한다.
반정규화는 특히 읽기 작업이 많은 시스템에서 유리하며, 조인(join)을 최소화하려는 경우에 사용된다.. 그러나 데이터 삽입, 수정, 삭제 시 중복된 데이터를 모두 업데이트해야 하므로 관리상의 문제가 발생할 수 있다.
예시:
학생과 수업 정보를 저장하는 테이블이 정규화되어 있다고 가정해보자.
정규화된 테이블:
- 학생 테이블:
| 학생ID | 학생이름 |
| 1 | 홍길동 |
| 2 | 이영희 |
- 수업 테이블:
| 수업ID | 수업명 |
| 101 | 수학 |
| 102 | 영희 |
- 학생_수업 테이블:
| 학생ID | 수업ID |
| 1 | 101 |
| 1 | 102 |
| 2 | 101 |
이 테이블에서 수업 정보와 학생 정보를 조회할 때는 여러 테이블을 조인해야 하므로 성능이 저하될 수 있다. 이를 반정규화하여 학생 테이블에 수업 정보를 직접 넣으면 조회 성능을 향상시킬 수 있다.
반정규화된 테이블:
| 학생ID | 학생이름 | 수업명 |
| 1 | 홍길동 | 수학 |
| 1 | 홍길동 | 영어 |
| 2 | 이영희 | 수학 |
반정규화된 테이블에서는 "수업명"이 중복되어 저장되므로 조회 시 조인이 필요 없고, 성능이 향상된다. 하지만 수업 정보가 변경될 때마다 모든 학생 레코드를 수정해야 하므로 유지보수 비용이 증가한다.
반정규화의 장점
- 성능 향상 (특히 조회 성능):
- 반정규화를 통해 데이터 중복을 허용하고 테이블을 합치면, 조인을 최소화할 수 있습니다. 이를 통해 조회 성능을 크게 향상시킬 수 있다.
- 예를 들어, 하나의 테이블에 데이터를 중복 저장하면, 여러 테이블을 조회하거나 조인하는 데 드는 시간을 줄일 수 있다.
- 디스크 I/O 감소:
- 데이터 조회 시 여러 테이블을 조인하는 대신 하나의 테이블에서 필요한 데이터를 바로 가져올 수 있기 때문에, 디스크 I/O를 줄일 수 있다.
- 단순한 쿼리 구조:
- 반정규화된 테이블에서는 단순한 쿼리로 데이터를 조회할 수 있기 때문에, 복잡한 조인 쿼리를 작성할 필요가 없습니다. 이는 쿼리 작성과 유지 보수에 있어서 더 단순하고 효율적일 수 있다.
정규화 (Normalization)
정규화는 데이터베이스 설계 과정에서 데이터를 효율적으로 분리하여 중복을 줄이고, 무결성을 유지하기 위한 방법입니다. 정규화의 목표는 데이터 중복을 없애고 데이터 일관성을 보장하는 것.
중복 데이터를 허용하지 않음으로써, 무결성을 유지하고, DB 저장 용량도 줄일 수 있다.
정규화는 여러 단계로 나뉘며, 각 단계는 정규형 (Normal Form)이라고 부릅니다. 가장 일반적으로 사용하는 정규형은 1~3 정규형이다.
1. 제 1 정규형 (1NF)
제 1 정규형은 "각 컬럼이 원자값(Atomic Value)을 가져야 한다"는 규칙.
즉, 각 열의 값은 더 이상 나눌 수 없는 단일 값이어야 하며, 복합적인 값이나 리스트, 집합 등을 컬럼에 저장할 수 없다.
예시:
학생ID 학생이름 수업명
| 1 | 홍길동 | 수학, 영어 |
| 2 | 이영희 | 수학, 과학 |
위와 같은 테이블에서는 "수업명"이 복합적인 값(수학, 영어, 수학, 과학)을 가집니다. 이를 1NF로 변환하려면, 각 수업을 별도로 분리하여 하나의 값만 들어가게 해야 한다.
1NF 변환 후:
| 학생ID | 학생이름 | 수업명 |
| 1 | 홍길동 | 수학 |
| 1 | 홍길동 | 영어 |
| 2 | 이영희 | 수학 |
| 2 | 이영희 | 과학 |
이렇게 각 값이 원자적(Atomic)인 값으로 변경되어야 제 1 정규형을 만족합니다.
2. 제 2 정규형 (2NF)
제2 정규화란 제1 정규화를 진행한 테이블에 대해 완전 함수 종속을 만족하도록 테이블을 분해하는 것이다. 여기서 완전 함수 종속이라는 것은 기본키의 부분집합이 결정자가 되어선 안된다는 것을 의미한다.
예시:
학생이 여러 수업을 듣는 경우, 학생ID와 수업ID를 기본 키로 가정한 테이블이 있다고 가정해보자.
| 학생ID | 수업ID | 학생이름 | 성적 |
| 1 | 101 | 홍길동 | 3.5 |
| 2 | 103 | 이영희 | 4.0 |
이 테이블에서 기본키는 (학생ID, 수업ID)로 복합키이다. 그리고 (학생ID, 수업ID) 기본키는 성적을 결정하고 있다.
그런데 여기서 교수이름이라는 컬럼은 기본키의 부분집합인 수업ID에 의해 결정될 수 있다. 그리고 학생이름이라는 컬럼도 기본키의 부분집합인 학생ID에 의해 결정될 수 있다.
즉, 기본키 (학생ID, 수업ID)의 부분키인 수업ID와이 결정자이기 때문에 위의 테이블의 경우 다음과 같이 기존의 테이블에서 강의실을 분해하여 별도의 테이블로 관리하여 제2 정규형을 만족시킬 수 있다.

2NF 변환 후:
- 수강 테이블:
| 학생ID | 수업ID | 성적 |
| 1 | 101 | 3.5 |
| 2 | 103 | 4.0 |
- 학생 테이블:
| 학생ID | 학생이름 |
| 101 | 홍길동 |
| 103 | 이영희 |
3. 제 3 정규형 (3NF)
제 3 정규형은 2NF를 만족한 상태에서 "이행적 함수 종속성(Transitive Dependency)을 제거해야 한다"는 규칙. 이행적 함수 종속성은 A -> B, B -> C일 때 A -> C가 성립하는 경우를 의미한다.
즉, 컬럼 간에 간접적인 종속성이 존재하면 이를 제거해야 한다.
예시:
| 학생ID | 지도교수 | 학과 |
| 1 | 김교수 | 컴퓨터학과 |
| 2 | 박교수 | 수학과 |

기존의 테이블에서 학생 ID는 지도교수를 결정하고 있고, 지도교수는 학과를 결정하고 있다. 그렇기 때문에 이를 (학생 ID, 지도교수) 테이블과 (지도교수, 학과) 테이블로 분해해야 한다.
이행적 종속을 제거하는 이유는 비교적 간단하다. 예를 들어 1번 학생의 지도교수가 박교수로 변경되었다고 하자. 이행적 종속이 존재한다면 1번의 학생의 지도교수님은 수학과가 되게 된다. (컴퓨터학과임에도)
3NF 변환 후:
- (학생 ID, 지도교수) 테이블
| 학생ID | 지도교수 |
| 1 | 김교수 |
| 2 | 박교수 |
- (지도교수, 학과) 테이블
| 지도교수 | 학과 |
| 김교수 | 컴퓨터학과 |
| 박교수 | 수학과 |
반정규화 (Denormalization)
반정규화는 정규화된 데이터베이스에서 성능을 향상시키기 위해 일부러 데이터를 중복하여 저장하는 과정이 이다. 이는 주로 조회 성능을 최적화하기 위해 사용된다. 데이터 중복이 발생할 수 있지만, 조회 속도를 빠르게 하는 장점이 존재한다.
반정규화는 특히 읽기 작업이 많은 시스템에서 유리하며, 조인(join)을 최소화하려는 경우에 사용된다.. 그러나 데이터 삽입, 수정, 삭제 시 중복된 데이터를 모두 업데이트해야 하므로 관리상의 문제가 발생할 수 있다.
예시:
학생과 수업 정보를 저장하는 테이블이 정규화되어 있다고 가정해보자.
정규화된 테이블:
- 학생 테이블:
| 학생ID | 학생이름 |
| 1 | 홍길동 |
| 2 | 이영희 |
- 수업 테이블:
| 수업ID | 수업명 |
| 101 | 수학 |
| 102 | 영희 |
- 학생_수업 테이블:
| 학생ID | 수업ID |
| 1 | 101 |
| 1 | 102 |
| 2 | 101 |
이 테이블에서 수업 정보와 학생 정보를 조회할 때는 여러 테이블을 조인해야 하므로 성능이 저하될 수 있다. 이를 반정규화하여 학생 테이블에 수업 정보를 직접 넣으면 조회 성능을 향상시킬 수 있다.
반정규화된 테이블:
| 학생ID | 학생이름 | 수업명 |
| 1 | 홍길동 | 수학 |
| 1 | 홍길동 | 영어 |
| 2 | 이영희 | 수학 |
반정규화된 테이블에서는 "수업명"이 중복되어 저장되므로 조회 시 조인이 필요 없고, 성능이 향상된다. 하지만 수업 정보가 변경될 때마다 모든 학생 레코드를 수정해야 하므로 유지보수 비용이 증가한다.
반정규화의 장점
- 성능 향상 (특히 조회 성능):
- 반정규화를 통해 데이터 중복을 허용하고 테이블을 합치면, 조인을 최소화할 수 있습니다. 이를 통해 조회 성능을 크게 향상시킬 수 있다.
- 예를 들어, 하나의 테이블에 데이터를 중복 저장하면, 여러 테이블을 조회하거나 조인하는 데 드는 시간을 줄일 수 있다.
- 디스크 I/O 감소:
- 데이터 조회 시 여러 테이블을 조인하는 대신 하나의 테이블에서 필요한 데이터를 바로 가져올 수 있기 때문에, 디스크 I/O를 줄일 수 있다.
- 단순한 쿼리 구조:
- 반정규화된 테이블에서는 단순한 쿼리로 데이터를 조회할 수 있기 때문에, 복잡한 조인 쿼리를 작성할 필요가 없습니다. 이는 쿼리 작성과 유지 보수에 있어서 더 단순하고 효율적일 수 있다.
