오늘은 유명한 유형 중 하나인 LIS 유형에 대해 정리해보고자 한다.
해당 유형을 안 지 얼마 되지 않았지만, 유형이 어느정도 정형화 되어있는 느낌이다. 해당 유형을 풀이하는 방법은 DP, 이분탐색 2가지가 있다.
DP로 풀이할 경우 O(N^2)의 시간복잡도를, 이분탐색으로 풀이할 경우 O(NlogN)의 시간복잡도를 가진다. 따라서 문제에 나와있는 조건을 잘 보고 시간복잡도를 따져서 알고리즘을 선택하는 것이 중요하다.
해당 유형은 가장 긴 증가하는 부분 수열의 길이까지만 구하거나, 더 나아가 부분 수열 자체를 출력해야하는 문제들이 있다.
해당 유형은 1,2편으로 나누어 작성하고자 하며, 해당 글(1편)에서는 가장 긴 증가하는 부분 수열의 길이까지만 구하는 문제를 다뤄보고자 한다.
우선 백준 12015번 문제를 통해 이해해보면, 문제를 푸는 단계는 아래와 같다.
- 배열을 순차적으로 탐색한다.
- 배열을 탐색하다가 해당원소가 LIS 배열의 가장 끝 원소보다 더 크다면, 뒤에 삽입한다.
- 그렇지 않다면, LIS 수열을 이루는 원소 중 탐색중인 원소보다 크거나 같은 원소를 처음 만나는 위치(-> lower_bound)를 찾고, 해당 위치에 원소를 삽입한다.
- → 이 과정에서 우리는 이분탐색을 사용한다. (해당 문제는 N이 최대 1,000,000 이므로 DP로는 풀이가 불가하다.)
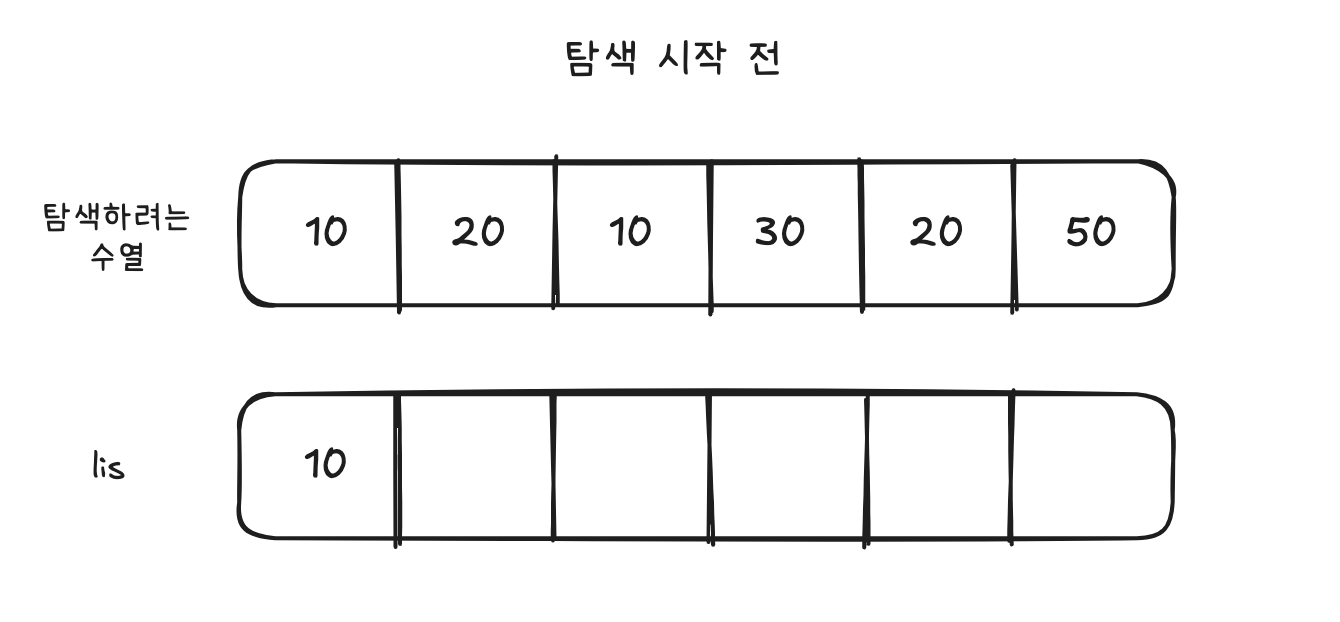
1. 1단계 (2번째 원소 10)
- LIS 배열의 가장 끝 원소인 10보다 크므로, 맨 뒤로 삽입한다.
- 참고) 풀이방법마다 다르지만, 나는 lis리스트에 먼저 10을 넣어놓고 시작했다.
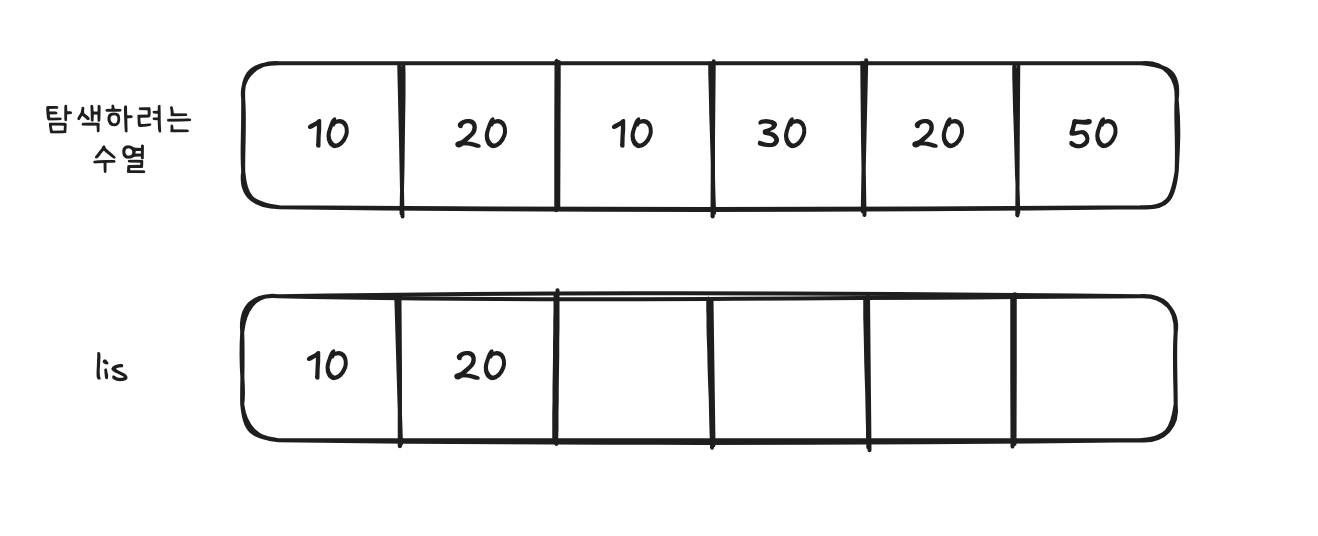
2. 2단계 (3번째 원소 10)
- LIS 배열의 가장 끝 원소인 10보다 작으므로 , 이분탐색을 통해 LIS 배열의 원소들 중 숫자 10보다 크거나 같은 원소를 가장 처음 만나는 위치를 찾는다. 여기서는 10이 존재하는 위치 0이다.
- LIS의 첫번째 위치에 10이 삽입된다. (변화x)
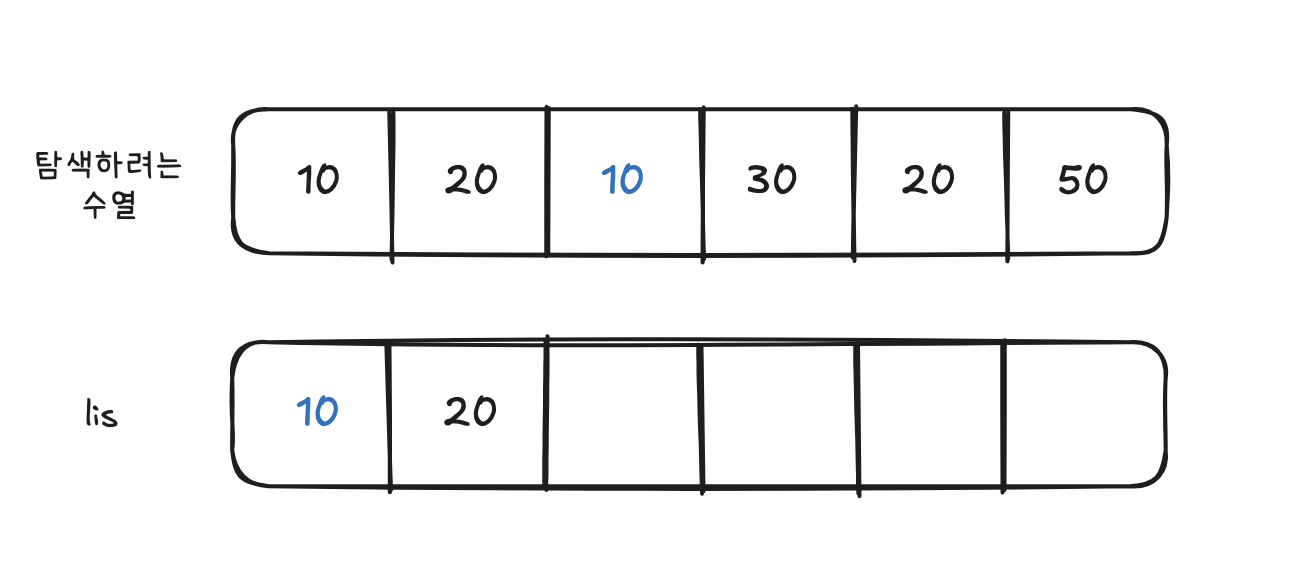
3. 3단계 (4번째 원소 30)
- LIS 배열의 가장 끝 원소인 20보다 크므로, 맨 뒤로 삽입한다.
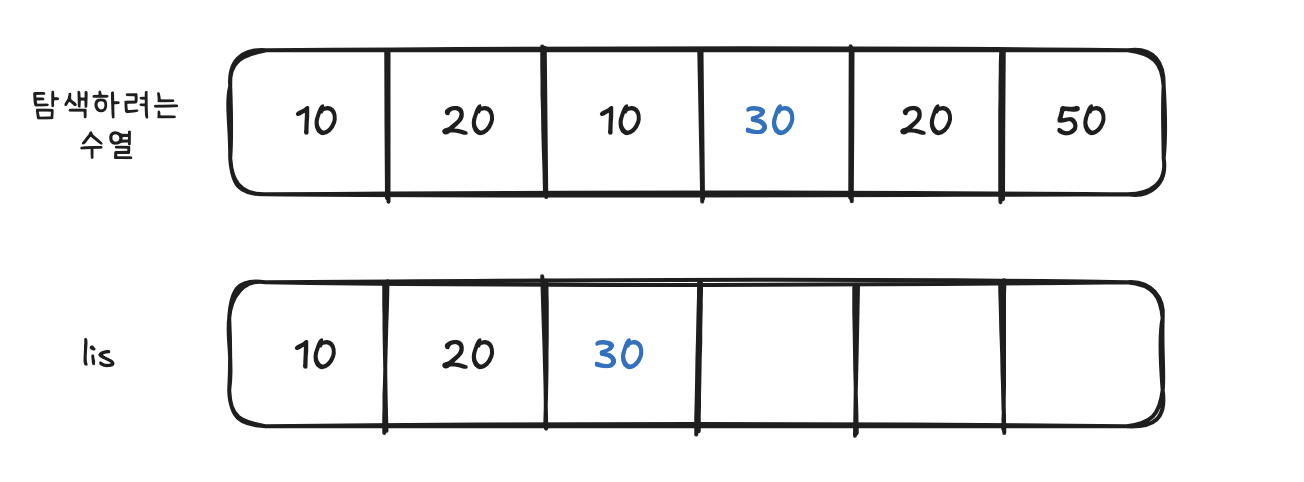
4. 4단계 (5번째 원소 20)
- LIS 배열의 가장 끝 원소인 30보다 작으므로 , 이분탐색을 통해 LIS 배열의 원소들 중 숫자 20보다 크거나 같은 원소를 가장 처음 만나는 위치를 찾는다. 여기서는 20이 존재하는 위치 1이다.
- LIS의 두번째 위치에 20이 삽입된다. (변화x)
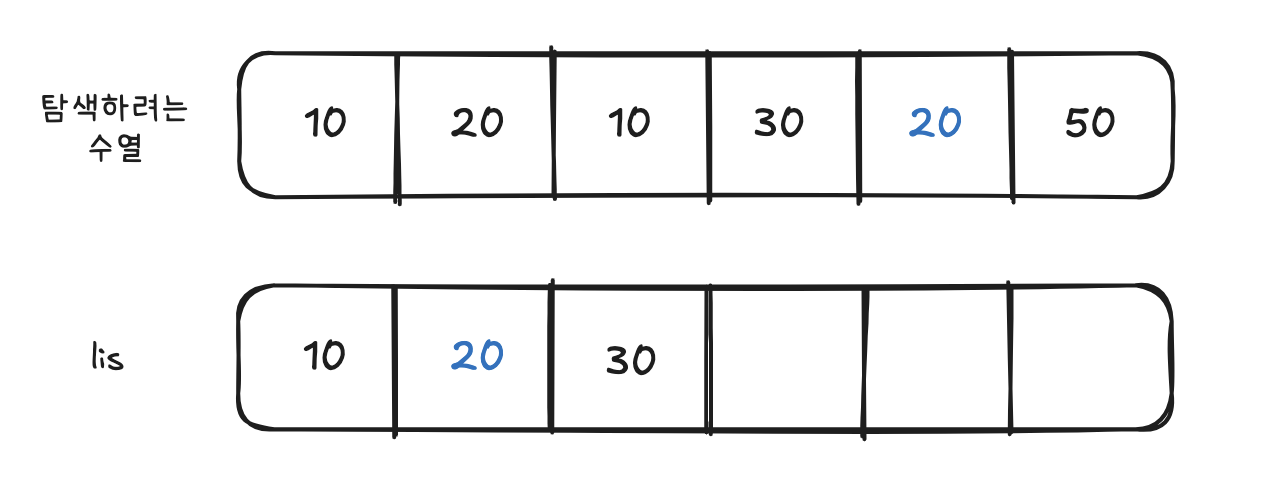
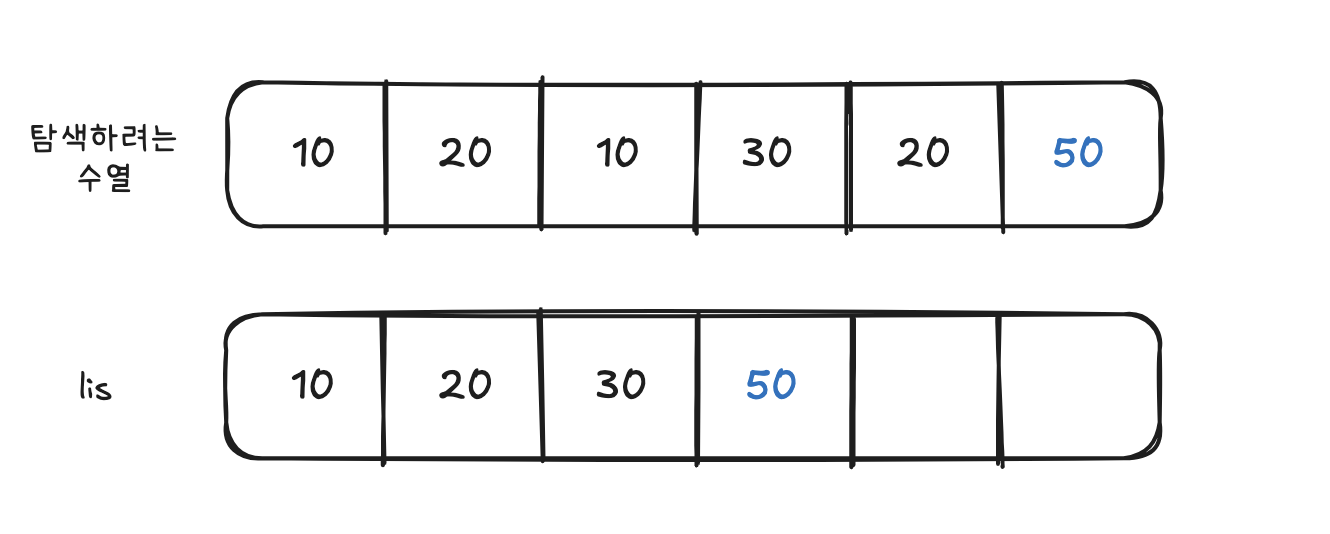
5. 5단계 (6번째 원소 50)
- LIS 배열의 가장 끝 원소인 30보다 크므로, 맨 뒤로 삽입한다.
lower_bound : 어떤 값 x보다 크거나 같은 값이 나오는 첫 위치입니다. python에서는 bisect_left()
upper_bound : 어떤 값 x보다 큰 값이 나오는 첫 위치입니다. python에서는 bisect_right()
이분 탐색으로 풀었을 때, 풀이코드는 아래와 같다.
이분 탐색 알고리즘을 실제 코드로 구현해서 풀 수도 있지만, 파이썬에서 이분탐색을 지원하는 bisect함수가 있어서 이걸 쓰면 훨씬 간단해진다.
import sys
import bisect
input = sys.stdin.readline
n = int(input())
nums = list(map(int, input().split()))
lis = [nums[0]]
for i in range(1, n):
target = nums[i]
if lis[-1] < target:
lis.append(target)
else:
idx = bisect.bisect_left(lis, target)
lis[idx] = target
print(len(lis))
-> 이분 탐색도 구현한 코드
import sys
input = sys.stdin.readline
n = int(input())
nums = list(map(int, input().split()))
def binary_search(target):
start, end = 0, len(lis)
while start <= end:
mid = (start + end) // 2
if lis[mid] == target:
return mid
elif lis[mid] < target:
start = mid + 1
else:
end = mid - 1
return start
lis = [nums[0]]
for i in range(1, n):
target = nums[i]
if lis[-1] < target:
lis.append(target)
elif lis[-1] > target:
idx = binary_search(target)
lis[idx] = target
print(len(lis))
-> 해당 문제는 시간초과로 인해 dp로 풀 수 있지만, 만약 푼다면 코드는 아래와 같다.
import sys
input = sys.stdin.readline
n = int(input())
nums = list(map(int, input().split()))
dp = [1] * n
for i in range(n):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
a = max(dp)
res = []
for i in range(n-1, -1, -1):
if dp[i] == a:
res.append(nums[i])
a -= 1
print(len(res))
이렇게 이분탐색으로 LIS의 길이를 푸는 방법을 알아보았는데, 첫번째 풀이대로하면 가장 긴 증가하는 부분 수열을 직접 구할 때 아래 예시처럼 문제가 생긴다. LIS의 길이뿐만 아니라 LIS 원소들을 알고 싶으면 어떻게 해야 할까? -> 이건 2편에서 다뤄보겠습니다!!
[예시]
주어진 수열: 1 7 3 2 5 10 3
실제 정답: 1 2 5 or 1 2 3
첫번째 풀이의 결과물: 1 2 3 10
도움 받은 글
가장 긴 증가하는 부분 수열(LIS) 완전 정복 - 백준 파이썬
최근 들어, 알고리즘에 재미를 붙였다. 백준 문제를 풀면 문제 난이도마다 티어가 올라가는 재밌는 사이트(solved.ac)가 생겨서 뭔가 동기 부여되는 것 같다. 언어는 python을 사용하고 있다. (취준
seohyun0120.tistory.com
'Coding > 코딩테스트 공부' 카테고리의 다른 글
| 백준 19238번 문제 - BFS & 구현 (0) | 2025.02.17 |
|---|---|
| [이.코.테] chap13. DFS/BFS - 특정 거리의 도시 찾기 (0) | 2022.07.29 |
| [이.코.테] chap11. 그리디 - 만들 수 없는 금액 (1) | 2022.07.20 |
| [코드 리뷰] 자료구조&알고리즘 - 2강 실습(2) 리스트에서 원소 찾아내기 (0) | 2022.06.28 |
| [알고리즘(Python)/코테공부] 뒤집은 소수 (0) | 2022.01.27 |
