[자료구조] 트리(Tree)
2021-2학기 자료구조 공부하면서 정리하는 내용
트리의 개념
: 1개 이상의 노드로 이루어진 자료구조
특징)
1) 최상위 노드는 루트 노드
2) 노드들은 원소가 중복되지 않는 n개의 부속트리를 갖는다.
3) 비순환 구조(사이클x), 계층구조를 이룬다.
필요성)
: 자료검색시 노드를 처음부터 찾아가는 단점 보완, 이진 검색의 장점 이용!
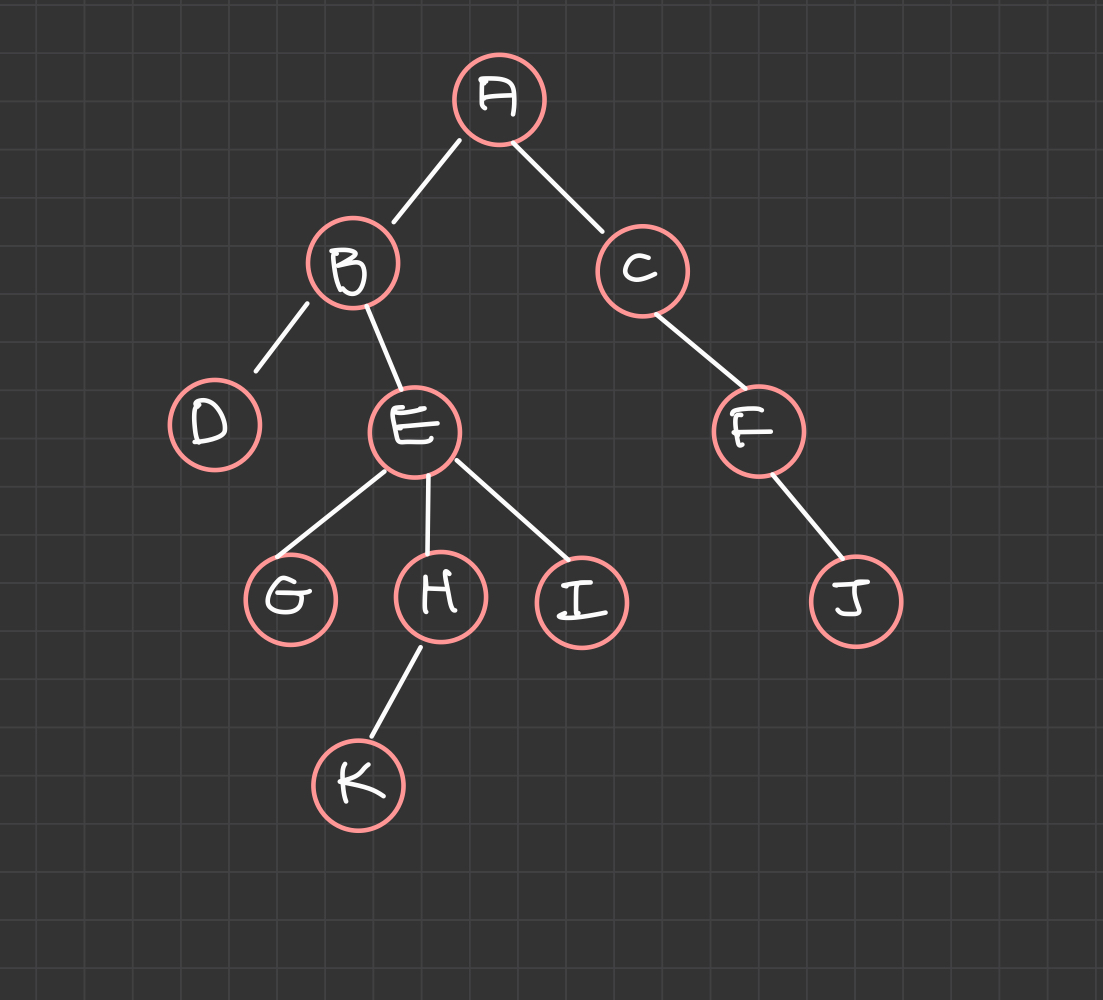
1. 트리의 용어
1.1. 노드
1) 부모노드 : 부속 트리를 가진 노드
노드 B의 부모노드 : 노드 A
2) 자식노드 : 부모에 속한 노드
노드 E의 자식노드 : 노드 G, H, I
3) 형제노드 : 부모가 같은 노드
노드 D의 형제노드 : 노드 E
4) 맆(단말)노드 : 차수가 0인 노드(자식노드x)
노드 D, G, K, I, J
1.2. 차수(degree)
1) 노드의 차수 : 노드의 하위(부속) 트리 개수(가지의 수 세기!)
노드 E의 차수 : 3 , 노드 B의 차수 : 2, 노드 J의 차수 : 0
2) 트리의 차수 : 트리의 최대 차수
노드 E의 차수가 3으로 트리의 최대 차수가 3이다.
1.3. 깊이(depth)
1) 노드의 깊이 : 루트에서 해당 노드까지의 간선의 수
노드 k의 깊이 : 4
2) 트리의 깊이 : 트리에 속한 노드의 최대 레벨
노드 k가 최대 레벨을 갖는다. 트리의 깊이는 5
*노드의 크기: 자신을 포함한 자식 노드의 개수
이진트리
: 각 노드가 2개 이하의 자식을 갖는 트리
특징)
1) 노드가 없는 트리도 이진 트리
2) 최대 레벨이 n일 때, 최대 노드의 개수는 2^n-1이다.
3) n0 = n2 + 1 (차수가 0인 노드: n0, 차수가 n1 인 노드: n1, 차수가 n2인 노드: n2)
n = 2xn2 + 1xn1 + 0xn0 + 1
n = n0 + n1 + n2
1. 이진트리의 종류
1) 스큐 이진 트리 : 한 쪽 방향으로만 노드를 갖는 트리
2) 포화 이진 트리 : 마지막 레벨까지 노드가 꽉 차 있는 트리
3) 완전 이진 트리 : 마지막 레벨-1까지는 노드가 꽉 차있고, 마지막 레벨은 왼쪽부터 노드가 차는 트리
2. 노드 최대, 최소 개수(트리의 깊이가 n)
1) 이진트리의 최소 개수 : 이진트리가 스큐트리일 때 , n개
2) 이진트리의 최대 개수 : 이진트리가 포화 이진 트리일 때, 2^n - 1개
3) 완전 이진 트리
이진트리의 저장
1. 배열을 이용
: 루트부터 순차적으로 배열에 저장
장단점)
장점: 노드의 위치를 인덱스를 통해 쉽게 알 수 있다.
단점: 스큐트리의 경우 빈 저장 공간이 많다. 효율적x
2. 연결리스트를 이용
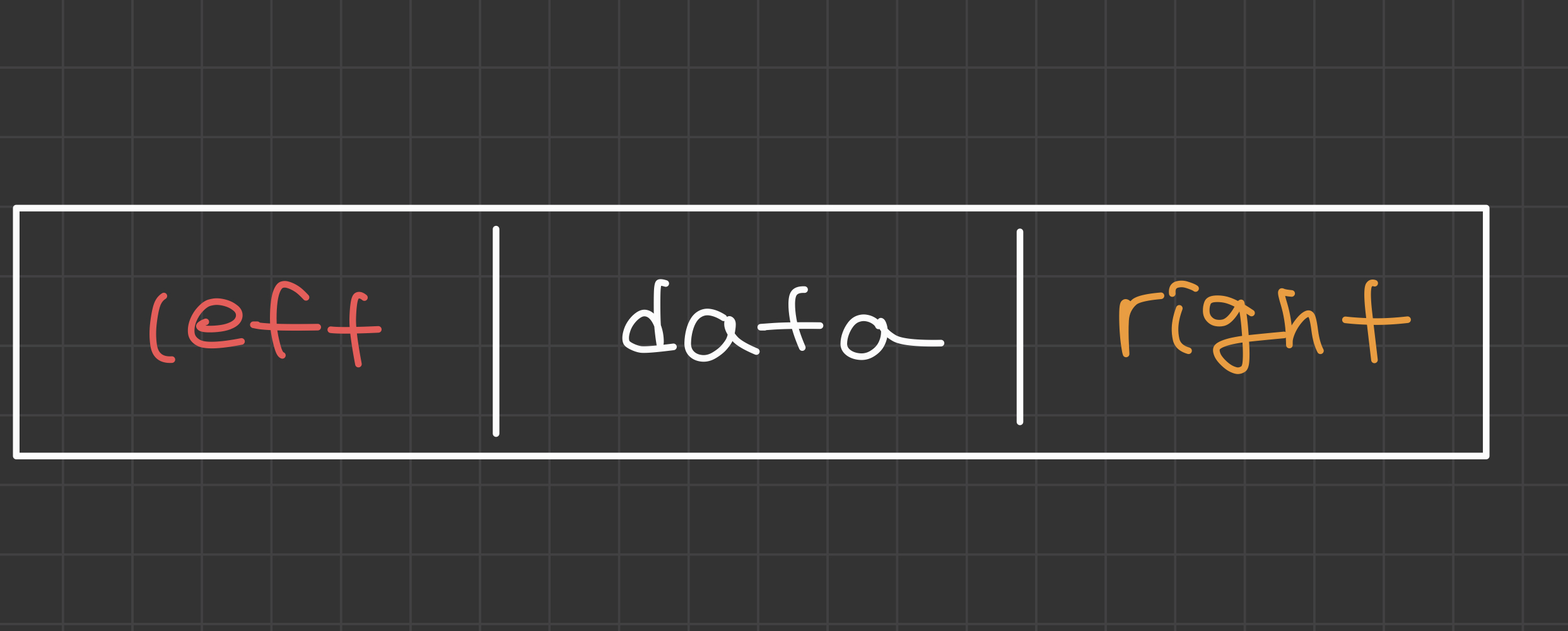
- left, right는 각각 왼쪽 부속 트리와, 오른쪽 부속 트리를 가리키는 포인터 필드